ESI/LS
From WikiZMSI
Regulamin zajęć laboratoryjnych
Zajęcia laboratoryjne z przedmiotu "Elementy sztucznej inteligencji" mają na celu zapoznanie słuchaczy z językiem programowania logiki - Prolog i zachęcenie do wykorzystania tego języka do oprogramowania problemów z dziedziny "sztucznej inteligencji".
Kurs obejmuje 15h lekcyjnych w blokach dwugodzinnych. W sumie w semestrze odbywa się 7 zajęć po 2h.
Obecność na zajęciach
Regulamin studiów Politechniki Szczecińskiej w rozdziale III, §10, ustęp 2 stwierdza: "Nieobecność studenta, nawet usprawiedliwiona na więcej niż 1/5 godzin obowiązkowej formy zajęć może być podstawą do niezaliczenia tej formy zajęć."
W myśl tego przepisu należy uczestniczyć w możliwie wszystkich zajęciach. Student ma prawo do nieobecności na jednych zajęciach laboratoryjnych.
Jeżeli z uzasadnionego powodu student nie może uczestniczyć w zajęciach własnej grupy może odpracować zajęcia z inną grupą. Musi jednak zostać spełniony warunek, że grupa realizuje program zajęć, które student opuścił.
Zachowanie na sprawdzianach
Regulamin studiów Politechniki Szczecińskiej w rozdziale III, §15, ustęp 3 stwierdza: "W szczególności, w przypadku stwierdzenia przez nauczyciela akademickiego, że student podczas egzaminu, zaliczenia, kolokwium lub innego sprawdzianu wiedzy korzystał z niedozwolonych form pomocy, nauczyciel ten może wystawić studentowi ocenę niedostateczną i wnioskować do dziekana o jego ukaranie."
Uprasza się zatem o nie korzystanie z pomocy pisemnych czy ustnych. Konsekwencje są określone w regulaminie.
Wpływ oceny z laboratorium na ocenę z wykładu
Wpływ oceny z laboratorium na ocenę z całego kursu (system punktowy) wynosi 50%. Aby uzyskać wpis z wykładu należy uzyskać pozytywną ocenę z laboratoriów.
Ocena z laboratoriów
Na ocenę końcową wpływać będzie:
- punktacja z wejściówek,
- aktywność na zajęciach.
ad 1. Każde zajęcia laboratoryjne rozpoczynają się wejściówką. Zakres materiału będzie podawany z przynajmniej dwutygodniowym wyprzedzeniem w niniejszym serwisie.
Na każdym sprawdzianie padną najwyżej trzy pytania lub zagadnienia do omówienia. Za każdą odpowiedź autor może uzyskać od 0 pkt (brak odpowiedzi lub odpowiedź nieprawidłowa) do 1 pkt (odpowiedź w pełni poprawna), co pozwala zgromadzić maksymalnie do 3 pkt za jedną wejściówkę.
Niektóre zadania praktyczne będzie można wykonywać z wykorzystaniem kompilatora Prologu.
Jeżeli student jest nieobecny na zajęciach i nie uczestniczy w równoważnych laboratoriach z inną grupą, nie może odrabiać samej wejściówki.
ad 2. W trakcie zajęć może być oceniana aktywność w skali od -1 do 1.
Punkty ujemne zdobywają studenci za niepoprawne zachowanie, ostentacyjne demonstrowanie braku zainteresowania zajęciami, brak wyników pracy zadanej do wykonania w trakcie zajęć, itp.
Punkty dodatnie przyznawane będą za wykazanie się wiedzą powyżej przeciętną, rozwiązanie dodatkowego problemu zadanego przez prowadzącego, itp.
Punkty zebrane przez studenta z wejściówek i aktywności zostaną zsumowane i podzielone przez maksymalną liczbę punktów z wejściówek. Powstały odsetek będzie wskazywał na ocenę zgdonie z poniższą listą:
- < 0 - 0.6 ) : niedostateczny
- < 0.6 - 0.68 ): dostateczny
- < 0.68 - 0.76 ): dostateczny plus
- < 0.76 - 0.84 ): dobry
- < 0.84 - 0.92 ): dobry plus
- < 0.92 - 1 >: bardzo dobry
Sytuacje wyjątkowe
Jeżeli z powodu choroby student przebywa na zwolnieniu ponad 2 tygodnie, tak, że nie może odpracować zajęć z inną grupą, przedstawiając odpowiednie zwolnienie będzie mógł poprawiać wejściówkę na konsultacjach.
Zaliczenia poprawkowe
Jeżeli student nie uzyska wystarczającej liczby punktów końcowych i uzyska ocenę niedostateczną ma prawo do dwóch poprawek w ciągu roku (Regulamin studiów PS rozdział V §22 ustęp 4). Pierwsza poprawa odbędzie sie w sesji poprawkowej, a druga pod koniec semestru zimowego.
Inne
- Wszelkie pytania, wątpliwości można rozwiązywać osobiście w czasie konsultacji lub drogą elektroniczną.
- Proszę pamiętać, że pomimo tego, ze korespondencja jest elektroniczna ciągle ma charakter formalny. Proszę zatem przestrzegać zasad pisania pism oficjalnych. Zaczynać list od powitania, kończyć formą grzecznościową i podpisywać się imieniem i nazwiskiem.
Laboratorium 1 --- wstęp do Prologu
Na zajęciach wykorzystywany będzie SWI Prolog. Oprogramowanie dostępne na serwerach Jota. Oficjalna strona SWI Prolog zawiera dokumentację jak i wersję kompilatora pod Linux'a i MS Windows.
Programowanie w Prologu - kilka użytecznych linków:
- strony w języku polskim:
- strony w języku angielskim:
Materiał na laboratoria jest głównie zaczerpnięty z książki "PROLOG Programming for Artificial Intelligence" Ivana Bratko (ISBN: 0-201-40375-7). W języku polskim dostępna jest pozycja "Prolog. Programowanie." autorstwa W.F. Clocksin i C.S. Mellish. wyd. Helion, Gliwice 2003.
Co należy wiedzieć zanim...:
- język deklaratywny i opisowy;
- programowanie symboliczne;
- obiekty i relacje (przykład: Ala ma kota. Pomiędzy obiektami Ala i kot istnieje relacja posiadania jednokierunkowa.);
- reguły opisują relacje na podstawie innych relacji. (przykład: Właściciel to ktoś kto coś posiada.).
- Program składa się z faktów i reguł zapisanych według odpowiedniej składni.
Zadania
Deklarowanie faktów
1. Uruchom kompilator Prologu
swiprolog lub swipl
2. Aby przejść w tryb wpisywania faktów i reguł wpisz
[user].
3. Aby zakończy tryb zapisywania reguł i przejść do trybu zapytań wpisz:
CTRL-D
4. Wpisz następujące fakty:
- Ala lubi koty.
lubi( ala, koty).
- Marek lubi psy.
lubi( marek, psy).
- Ala jest kobietą.
kobieta( ala).
- Marek jest mężczyzną.
mezczyzna( marek).
Zapytania
1. W trybie zapytań zadaj pytania do wprowadzonych faktów:
- Czy Ala lubi koty?
lubi( ala, koty).
- Czy Marek jest kobietą?
kobieta( marek).
- Czy Jan jest mężczyzną?
mezczyzna( jan).
- Czy psy lubią Marka?
lubi( psy, marek).
2. Zadaj pytania ze zmiennymi:
- Czy jest coś co lubi Ala?
lubi( ala, X).
- Czy wiesz coś o istnieniu kobiet?
kobieta( Y).
- Czy psy są przez kogoś lubiane?
lubi( Ktos, psy).
Tworzenie pliku źródłowego
Stwórz w dowolnym edytorze plik tekstowy z rozszerzeniem pl i wpisz wcześniej zadane w trybie [user] fakty. Wczytaj w kompilatorze plik podając w linii zapytań
[nazwa_pliku].
Zadaj pytania złożone:
- Czy Ala lubi koty i Marek lubi koty?
lubi( ala, koty),lubi( marek, psy).
- Czy Ala jest kobietą i Marek jest mężczyzną?
kobieta( ala), mezczyzna( marek).
Dodaj do pliku pl fakt, że Marek lubi koty i ponownie skompiluj.
- Czy jest coś co lubi zarówno Ala jak i Marek?
lubi( ala, X), lubi( marek, X).
Dodawanie reguł
1. W pliku pl dopisz reguły:
- Marek lubi kobiety.
lubi( marek, X) :-
kobieta( X).
- Ala lubi to co Marek.
lubi( ala, X) :-
lubi( marek, X).
2. W trybie zapytań zapytaj:
- Co lubi Ala?
lubi( ala, X).
- Co lubi Marek?
lubi( marek, X).
Zależności rodzinne
- Pobierz plik źródłowy do zależności rodzinnych ⇒ Rodzinka.pro
- Narysuj graf zależności pomiędzy osobami.
- Skompiluj źródło swipl -o rodzinka -c Rodzinka.pro . W wyniku powstanie plik wykonywalny rodzinka. Po uruchomieniu można zadawać pytania do faktów wpisanych w źródłowej bazie wiedzy.
- Dodaj do źródła następujące reguły.
- Potomek offspring, to relacja odwrotna do rodzica parent.
- Matka mother, to rodzic parent płci żeńskiej female.
- Dziadek grandparent, to rodzic parent czyjegoś rodzica parent.
- Siostra sister, to ktoś kto ma tego samego rodzica parent i jest kobietą female.
- Przodek predecessor - poprzez rekurencyjne sprawdzanie poprzednich pokoleń rodziców parent.
Jak Prolog odpowiada na pytania
Zapisane w źródle fakty i reguły analizowane są od góry do dołu w kolejności wprowadzenia. Szukany jest fakt potwierdzający zapytanie. Jeżeli w pytaniu jest zmienna, to w trakcie wyszukiwania odpowiedzi jest ukonkretniana (podstawiane są pod nią stałe wartości - atomy). Jeżeli zapytanie jest złożone, to zawsze poszukuje się potwierdzenia predykatów od lewego do skrajnie prawego. Powrót do wcześniejszych predykatów celem sprawdzenia wszystkich kombinacji nazywa się nawracaniem (backtracking). (Szczegóły w literaturze)
Zadanie domowe
- Do przeczytania: W.F. Clocksin i C.S. Mellish. "Prolog. Programowanie." - Rozdział 1.
- Dokładnie przeanalizować wnioskowanie na przykładach. Dlaczego predykat siostra daje odpowiedź, że każda kobieta, która ma rodzica jest dla siebie siostrą?
- Jak inaczej można zdefiniować przodka by analiza odbywała się w przeciwnym kierunku?
- Zastanowić się i sprawdzić jak można zdefiniować inne zależności rodzinne (rodzeństwo, ciotka, itd...)
- Przygotować się ze składni Prologu.
- Wyszukać za pośrednictwem Internetu jakie aplikacje programuje się w Prologu - aktualne zastosowania.
Laboratorium 2 --- Debugowanie programów. Termy, unifikacja, arytmetyka.
Kontrola poprawności programu
SWI Prolog zawiera następujące porty w trybie debugowania predykatu: wejściowe: call, redo i wyjściowe: fail, exit, exception.
Debugger wykonuje program krok po kroku i wywołuje predykat poleceniem call. Powrót z predykatu może nastąpić w dwojaki sposób exit: sukces, lub predykat zawodzi: fail. Jeżeli pojawia się wyjście typu fail to wykonuje się nawrót do sprawdzania predykatu z możliwą do ustalenia alternatywną wartością. Predykat jest wówczas ponownie wywoływany redo. Sytuacje wyjątkowe są sygnalizowane przez exception.
Dodatkowy port unify pozwala obserwować unifikację.
Zadania (debugowanie):
Zadanie 1 - debugowanie może się odbywać w dwóch trybach [trace] (zatrzymanie się na każdym porcie) lub [debug] zatrzymanie się na ustawionych pułapkach. Wejście do trybów odpowiednio
trace.
i
debug.
Predykaty wbudowane: debugging/0, nodebug/0, notrace/0 kontrolują i zamykają tryby śledznia.
1. Wczytać źródło: Family.pro (plik pochodzi z książki I. Bratko).
2. Uruchomić tryb śledzenia [tracer]. Wywoła to procedurę śledzenia odpowiedzi na zadane zapytanie.
3. Zadać zapytanie
mother(pat,jim).
Prześledzić dowodzenie jego prawdziwości.
4. Dodać punkt śledzenia (pułapka) predykatem wbudowanym spy/1 np.
spy(female).
dla zapytania mother(pat,jim). UWAGA! Należy pozostać w trybie [debug]. Polecenie zdejmujące punkt śledzenia nospy/1 np.
nospy(female).
5. Zadać zapytanie
mother(X,jim).
Prześledzić dowodzenie jego prawdziwości.
6. Wypróbować następujące jednoznakowe polecenia podczas śledzenia:
- h(elp) ,
- L(isting),
- s(kip) --- przejdź do portu wyjściowego (fail, exit) ,
- a(bort),
- f(ail) - ustaw 0 dla danego predykatu,
- g(oal) - lista uzgadnianych predykatów,
- n(o debug) - wyjście z trybu śledzenia,
- + (spy) - załóż punkt śledzenia na aktualnym predykacie,
- - (no spy) - zdejmij punkt śledzenia z aktualnego predykatu,
- l(leap) - skok do pułapki.
Zadanie 2
1. Przetestować na bazie wiedzy Family.pro
2. Wpisać polecenie
visible(+all) , leash(-exit).
Nakazuje ono wypisywanie wszystkich portów i zatrzymywanie się w każdym porcie za wyjątkiem exit.
3. Uruchomić tracer.
4. Sprawdzić jak uzyskuje się odpowiedź na zapytanie
predecessor(X,jim).
Typy danych i operatory arytmetyczne
Prolog nie wymaga deklarowania typów. Zostaje on rozpoznany ze składni. Plik źródłowy składa się z termów, czyli:
- atomów: np. ala, x25, x_, x_y, 'Jan Kowalski', 1, -97, 3.14, -0.000035
- zmiennych: X, Wynik, _x23, specjalna zmienna anonimowa: _.
- struktur: składają się z kilku komponentów np. data(1, maj, 2004), data(Data, maj, 2004), odcinek(punkt(X,Y), punkt(X1,Y2)), par(r1,seq(r2,r3)).
Lista operatorów arytmetycznych i porównania:
- + dodawanie
- - odejmowanie
- / dzielenie
- // dzielenie całkowite
- * mnożenie
- ** potęga
- mod reszta z dzielenia
- is znak równości (wynik obliczeń arytmetycznych) np. ( X is 1 mod 3. )
- =:= czy wartości równe
- =\= czy wartości różne
- > większe
- < mniejsze
- >= większe równe
- =< mniejsze równe
Zadania (typy danych i operacje arytmetyczne):
1. Na źródle Family.pro wypróbować zapytania:
parent(X,_). mother(_,_). mother(X,X).
Jak należy je interpretować?
2. Korzystając ze zmiennej anonimowej dodać do pliku o zależnościach rodzinnych predykaty ma_dziecko/1, który wskaże imię osoby mającej potomstwo i ktos_jest_dziadkiem/0 sprawdzający czy istnieje obiekt spełniający relację dziadek.
3. W nowym pliku zapisać dwa fakty:
pionowy(odcinek(punkt( X, Y1), punkt( X, Y2))). poziomy(odcinek(punkt( X1, Y), punkt( X2, Y))).
- Jak należy interpretować zapisaną wiedzę?
- Narysować drzewko dla predykatów umieszczając w korzeniu pionowy lub poziomy. Ile argumentów ma relacja poziomy a ile struktura odcinek itd.
- Sprawdzić, czy punkty o współrzędnych (1,2) i (1,1) tworzą odcinek pionowy.
- Jakie współrzędne musi mieć drugi punkt, by tworzył poziomą z punktem (2,3)?
- Zapytać czy odcinek rozpoczynający się w punkcie (X1,Y1) i kończący w punkcie (X2,Y2) może być jednocześnie poziomy i pionowy. Czy odpowiedź jest poprawna?
4. Dane są struktury: punkt w 2D p2(X,Y) i punkt w 3D p3(X,Y,Z). Zdefiniować predykat obliczający kwadrat odległości pomiędzy punktami. np. na zapytanie:
kw_odleglosci(p2(1,2),p2(3,5),D).
uzyska się odpowiedź:
D=13 Yes
bo (3-1)**2 + (5-2)**2).
Unifikacja i porównywanie termów
Wpisanie w Prologu (czy to w trybie zapytań, czy w treści reguły) X = ala. oznacza unifikację (uzgodnienie). Co oznacza, że jeżeli można uczynić X i ala równymi to zwracamy sukces, gdy nie, porażkę. Gdy np. operacja == polega na sprawdzeniu równości termów. Sprawdzenie nierówności termów wykonuje się operatorem: \==.
Zadania z unifikacji i porównywania:
Wypróbować w trybie zapytań działanie: unifikacji i jej negacji(=, \=), równości i nierówności termów (==, \==) oraz przyrównania wartości arytmetycznych (=:=, =\= ):
X = ala. X = Y. ala = ola. X = data(1, maj, 2004). data(D, maj, 2003) = data(1, maj, 2004). data(D, maj, 2003) = data(1, maj, R). fun(X) = fun(fun(X)). 3 = 3. 1+2 = 3. 1+2 =:= 3. ala == ala. X == Y. X == X. 2+1 == 1+2. ala \== ola. odcinek( punkt( 1, 2), punkt( A)) = odcinek( B, punkt( 1, 2)). odcinek( punkt( 1, 2), punkt( A,B)) = odcinek( B, punkt( 1, C)).
Program na liczenie największego wspólnego dzielnika
Dane są dwie liczby całkowite dodatnie X i Y. Największy wspólny dzielnik D można określić sprawdzając trzy warunki (trzy reguły):
- Jeżeli X i Y są sobie równe, to D jest równe X.
- Jeżeli X<Y, to D jest równe największemu dzielnikowi z liczby X i różnicy Y-X. (w Prologu można zapisać jako regułę: nwd(X,Y,D) :- X < Y, Tmp is Y - X, nwd(X, Tmp, D).).
- Jeżeli Y<X, to postępujemy jak w punkcie 2 tylko ze zmienioną kolejnością argumentów.
Zdefiniować predykat nwd/3, który będzie spełniony, gdy trzeci argument będzie największym wspólnym dzielnikiem argumentu pierwszego i drugiego. Przykład wywołania:
nwd(5, 10, X).
Odpowiedzią będzie
X = 5 Yes
Wykorzystaj wbudowany predykat number/1, aby sprawdzać czy term jest liczbą.
Wyznaczanie ścieżki przejścia w acyklicznym grafie
Dowolny skierowany graf można zdefiniować podając parami łączone węzły. Niech tą relację opisuje predykat krawedz/2 np.
krawedz(a,b).
Przykład grafu:
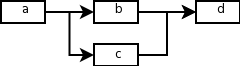Podać strukturę grafu z rysunku lub innego zaproponowanego za pomocą faktów z wykorzystaniem relacji krawedz/2.
Zdefiniować predykat sciezka/2, który będzie sprawdzał, czy istnieje ścieżka pomiędzy podanymi jako argumenty dwoma węzłami w grafie (analogiczne do definicji przodka w zależnościach rodzinnych).
Zadanie domowe
1. Do przeczytania: W.F. Clocksin i C.S. Mellish. "Prolog. Programowanie." - Rozdział 2.
2. Zadania do wykonania - bez sprawozdania
2.a Zadania z badania kolejności wykonywanych operacji:
- W pliku Wnioskowanie.pro zapisanych jest osiem klauzul. Zadać pytania:
dark(X),big(X). big(X),dark(X).
przy włączonym trybie śledzenia (trace). Bez trybu trace nie widać różnicy! Rozrysować graf odpowiedzi na podstawie analizy kolejności sprawdzania reguł. Jaka jest liczba nawrotów w jednym i drugim przypadku? PODPOWIEDŹ: zawsze zaczyna się od potwierdzenia prawdziwości pierwszego członu koniunkcji.
- W pliku Przodek.pro zapisane są różne warianty rekurencyjnej klauzuli przodek. Należy wpisać je do swojego pliku na zależności rodzinne uruchomić i sprawdzić różnicę w działaniu 4 różnych definicji predykatu? Sprawdzić na pytaniach
predecessor(X,jim). predecessor(bob,Y).
2.b Zadanie kolorowanie mapy
Stworzyć dowolną mapę terytorialną np.:
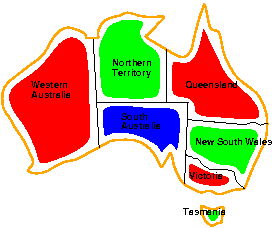Napisać program, który koloruje mapę z użyciem czterech kolorów, w taki sposób, by dwa sąsiadujące państwa/dzielnice nie miały tego samego koloru (tak jak na rysunku).
Podpowiedź: Państwa(stany) reprezentowane są przez zmienne. Cztery kolory wpisane są jako fakty. Wywołanie poprzez wprowadzenie zapytania np.
fill(Wester, Northern, South, Queensland, NSW, Victoria, Tasmania).
Kolory powinny być przypisane do państw (odpowiednich zmiennych). Należy wyznaczyć, jakie kraje (stany) nie mogą leżeć obok siebie tj. jakie zmienne nie mogą być sobie równe. Programik jest bardzo ograniczony: działa dla jednej konkretnej mapy.
Laboratorium 3 i 4 --- Listy jako specjalne struktury
Lista to ciąg uporządkowanych elementów. Elementy mogą być dowolnego typu. Listy można przedstawić w postaci drzewa. Lista jest strukturą o nazwie "." .
Przykłady list:
.(ala,[]) .(ala, .(narty, .(ksiazki, []))) .(head, .(tail,[]))
Łatwiejszy sposób notacji:
[ala] [ala,narty,ksiazki] [head,tail] [a,V,1,[c,s],p(X)] [1,2,3,4]
Sprawdzić w trybie zapytań następujące unifikacje:
.(a,.(b,.(c,[]))) = [a,b,c]. .(a,.(B,.(C,[]))) = [a,b,c]. [a,V,1,[c,s],p(X)] = [A,B,C,D,E]. [1,2,3,4] = [1|[2,3,4]]. [1,2,3,4] = [1,2|[3,4]]. [1,2,3,4] = [1,2,3|[4]]. [1,2,3,4] = [1,2,3,4,[]]. [1,2,3,4] = [1|2,3,4]. [Head|Tail] = [1,2,3,4]. [Head|Tail] = [[1,1,ala],2,3,4]. [Head|Tail] = [X+Y,x+y]. p([_,_,_,[_|X]]) = p([ala, ma, bardzo, [malego, burego, kotka]]).
Operacje na listach
1. Sprawdzenie czy element jest na liście (2 argumenty):
- Procedura: X jest elementem listy L jeżeli X jest głową listy L lub X jest elementem ogona listy L.
element(X,[X|_]). element(X,[_|Ogon]) :- element(X,Ogon).
- Sprawdzić działanie procedury dla przykładów:
element(a,[b,c,[s,a],a]). element(a,[b,c,[s,a]]). element([s,a],[b,c,[s,a]]). element(X,[a,b,c]). element(a, X).
- Istnieje wbudowany predykat działający w podany sposób: member/2
2. Łączenie list (3 argumenty):
- Procedura: Jeżeli pierwszy element listy jest pusty [], to drugi i trzeci element muszą być takie same (L = L). Natomiast jeżeli pierwszy element nie jest pusty, to musi posiadać głowę i ogon i głowę dodaje się do elementu trzeciego (lista połączona) jako głowę.
polacz([],L,L). polacz([X|L1],L2,[X|L3]) :- polacz(L1,L2,L3).
- Sprawdzić działanie procedury dla przykładów:
polacz([b,c,[s,a],a],[a],X). polacz([a],[b],[a,b]). polacz(L1,L2,[b,c,[s,a]]).
Ostatni działa jak dekompozycja listy.
- Istnieje wbudowany predykat działający w podany sposób: append/3
3. Usuwanie z listy (3 argumenty):
- Procedura: Jeżeli X jest w głowie listy, to wynikiem będzie ogon listy. Natomiast jeżeli X jest w ogonie to rekurencyjnie przeszukaj ogon.
usun(X,[X|L1],L1). usun(X,[Y|L2],[Y|L3]) :- usun(X,L2,L3).
- Sprawdzić działanie procedury dla przykładów:
usun(a,[s,a],X). usun(a,[a,b,a,a],X).
Istnieje wiele rozwiązań
usun(a,L,[d,s,e]).
Dodaje element do listy!
- Istnieją wbudowane predykaty usuwające elementy: delete/3 i select/3. Sprawdzić różnicę. Jak użyć select/3 do dodawania elementu do listy.
4. Podlista z listy (2 argumenty):
- Procedura: Jeżeli S jest podlistą L, to L może być zdekomponowana na na dwie listy L1 i L2 i L2 może być zdekomponowana na S i L3.
podlista(S,L) :- append(L1,L2,L), append(S,L3,L2).
- Uwaga: L1 i L3 mogą być zmiennymi anonimowymi
- Sprawdzić działanie procedury dla przykładów:
podlista([a,b],[a,b,c,d]). podlista(X,[a,b,c,d]).
- Istnieje wbudowany predykat działający w podany sposób: sublist/2, ale tylko w gprologu
5. Sprawdzić dostępne wbudowane predykaty dotyczące list poleceniem:
apropos(list).
Zadania na listach
- Lista ma zawierać miesiące. Zdefiniować predykat wyświetlający wszystkie miesiące przed i po podanym nazwą miesiącu. Należy wykorzystać append/3. Rozwiązanie
- Lista ma zawierać miesiące. Zdefiniować predykat wyświetlający jeden miesiąc przed i jeden po podanym nazwą miesiącu. Należy wykorzystać append/3. Rozwiązanie
- Dla podanej listy wyświetl tylko 3 początkowe elementy. Rozwiązanie
- Dla podanej listy wyświetl tylko 3 ostatnie elementy. Rozwiązanie
- Zdefiniować predykat element listy (member) za pomocą append/3. Rozwiązanie
- Zdefiniować predykaty: parzysta(Lista) i nieparzysta(Lista), które zwrócą wartość true, jeżeli argument jest odpowiednio listą z parzystą lub nieparzystą liczbą elementów. np. nieparzysta([a,b,c,d]). daje odpowiedź no, a parzysta([a,b,c,d]).daje odpowiedź yes. Rozwiązanie
- Zdefiniować relację odwrotna(Lista,Lista_odwrotna), zmieniająca kolejność elementów, np. odwrotna([a,b,c,d],[d,c,b,a]). Rozwiązanie
- Zdefiniować predykat palindrom(Lista). Lista jest palindromem, jeżeli czytając ją wspak uzyskamy taką samą kolejność elementów. Rozwiązanie
- Zdefiniować relację shift(Lista1, Lista2) przesuwającą pierwszy element lisy na jej koniec. Rozwiązanie
- Zdefiniować relację slownie(Lista1, lista2) podającą słowne odpowiedniki liczb zadanych listą, np. slownie([1,3,4],Y). Y=[jeden, trzy, cztery]. Wykorzystaj fakty slowo(1,jeden)., slowo(2,dwa). itd.. Rozwiązanie
- Zdefiniować predykat maxlista(Lista, Max) znajdującą największą wartość w liście liczbowej. Rozwiązanie
- Zdefiniować predykat sumalisty(Lista,Suma) obliczający sumę elementów listy, jeżeli są liczbami. Rozwiązanie
- Zdefiniować predykat lista_rosnaca(Lista), który daje odpowiedź yes jeżeli kolejność elementów jest rosnąca. Rozwiązanie
Zadanie domowe
- Do przeczytania: W.F. Clocksin i C.S. Mellish. "Prolog. Programowanie." - Rozdział 3.
Laboratorium 5 --- Odcinanie. Negacja przez niepowodzenie
Odcinanie oznaczane jest znakiem:
!
Jest operatorem do kontrolowania nawracania w Prologu. Dzięki jego umiejętnemu wykorzystaniu można zwiększyć efektywność kodu poprzez zmniejszenie liczby sprawdzanych warunków.
Zadania prezentujące zastosowania operatora !:
1. Napisać predykat funkcja/2, który nie zawiedzie, gdy pierwszy argument X i drugi argument Y przyjmą wartości opisane warunkami:
- Jeżeli X <3, to Y = 0.
- Jeżeli X ≥ 3 i X < 6, to Y = 2.
- Jeżeli X ≥ 6, to Y = 4.
Zadać pytanie:
funkcja(1,Y),Y > 2.
Jaki jest schemat odpowiedzi? Kiedy nastąpią nawroty? Wykorzystać polecenie trace.
2. W pliku Funkcja.pro znajduje się wersja programu rozwiązująca zadanie 1 z wykorzystaniem operatora !. Zadać to samo zapytanie jak w punkcie 1 i sprawdzić jaka jest różnica w udzielanej odpowiedzi. Wykorzystać polecenie trace.
3. Aby zwiększyć optymalność kodu można zapisać źródło w postaci następujących reguł:
- Jeżeli X<3, to Y = 0.
- W przeciwnym przypadku jeżeli X < 6, to Y = 2.
- W przeciwnym przypadku Y = 4.
Co doprowadza do źródła postaci: Funkcja_o.pro
4. Usunąć znaki odcięcia w kodzie w punktu 3 i zaobserwować jak w nowej wersji zachowywałby się predykat funkcja.
5. Dany jest program. Wykonać dla programu zadania:
5.1. Narysować drzewo zależności pomiędzy predykatami. W korzeniu:
top( X, Y)
a w liściach fakty.
5.2. Jaka będzie odpowiedź na pytanie
top( X, Y).
Ważne są wszystkie odpowiedzi i ich kolejność.
5.3. Używając trace zaznaczyć punkty nawrotów (redo) w drzewie. Ile jest nawrotów?
5.4. Zamienić
true(1)
na
!
Powtórzyć zadania z punktów 5.2. i 5.3. Jaki fragment drzewa został odcięty z przeszukiwania?
5.5. Zamienić
true(2)
na
!
Powtórzyć zadania z punktów 5.2. i 5.3. Jaki fragment drzewa został odcięty z przeszukiwania?
6. Napisać predykat max/3, który nie zawodzi, gdy trzeci argument jest większą z podanych w argumentach pierwszym i drugim liczb. Zastosować odcięcie. Co zmienia zastosowanie odcięcia?
7. Zdefiniować predykat element/2 sprawdzający, czy zadany element jest na liście. Stosując odcięcie powinniśmy zapewnić, że jak tylko rozwiązanie jest znalezione, to dalsze przeszukiwanie jest zbyteczne. Kiedy widać różnicę w działaniu wbudowanego predykatu member i zdefiniowanego w niniejszym zadaniu?
8. Zdefiniować predykat dodaj/3 dodający element na początku podanej listy. Predykat nie zawodzi, gdy 3 argument to lista zawierająca wynik połączenia. Dodanie powinno nastąpić tylko wówczas, gdy elementu nie ma jeszcze na liście, w przeciwnym wypadku jako wynik wyświetlamy listę zadaną. Stosując odcięcie powinno się zapewnić, że jak tylko sprawdzone zostanie, że element jest na liście, to dalsze przeszukiwanie jest zbyteczne. Porównać zachowanie predykatu dodaj/3 z operatorem i bez operatora obcięcia.
9. Wpisać polecenie w trybie zapytań
help(->).
W pliku Elseif.pro pokazane jest zastosowanie operatora ->.
Stosowanie negacji w Prologu
Negacja znana z rachunku zdań czy rachunku predykatów w Prologu nie występuje. Istnieje jednak operator
\+
który zdaje się działać podobnie. Działanie tego operatora jest oparte na wykorzystaniu operatora odcinania i wbudowanego predykatu fail/0.
Zadania prezentujące zastosowania operatora \+:
1. Przykład wykorzystania złączenia !,fail działającego podobnie do negacji. Predykat opisujący zdanie: Ala lubi wszystkie zwierzęta oprócz węży: dany jest w pliku Ala.pro. Zadać zapytania:
lubi(ala,waz). lubi(ala,kot).
2. Stosując !,fail jako negację zdefiniować predykat rozne/2, który nie zawodzi, gdy dwa elementy są różne.
3. Definicja operatora \+ dana jest w pliku Not.pro. Przeanalizować jego działanie. Wpisać polecenie w trybie zapytań
help(not).
Sugeruje się jednak stosowanie operatora \+.
4. Zmienić predykat z zadania 1 i 2 stosując operator \+ zamiast !,fail. Czy jest różnica w działaniu?
Problemy z zastosowaniem odcinania
Stosowanie operatorów ! i \+ ma plusy i minusy. Zaletą jest zwiększenie efektywności programu i możliwość stosowania reguł zależnych: jeżeli... w przeciwnym przypadku...
Zastosowanie operatora odcięcia zmienia logicznie (deklaratywnie) zdanie. np.:
p :- a, b. p :- c.
jest równoważne zdaniu:
p ⇔ (a &b) ∨ c.
Natomiast:
p :- a, !, b. p :- c.
co jest równoważne zapisowi:
p ⇔ (a &b) ∨ (~a & c).
Należy pamiętać, że negacje działają poprawnie tylko dla zunifikowanych zmiennych.
Przykład problemu wynikającego ze stosowania operatora \+ należy prześledzić wykorzystując plik z danymi: Rest.pro. Do pliku należy zadać zapytania:
wysoki_standard(X), polecana(X). polecana(X), wysoki_standard(X).
Jakie są odpowiedzi i dlaczego?
Zadanie domowe
Do przeczytania: W.F. Clocksin i C.S. Mellish. "Prolog. Programowanie." - Rozdział 4.
Laboratorium 6 --- przykłady zadań
Obliczanie oporności układu
Oporniki R1 i R2 mogą być połączone szeregowo i rezystancja zastępcza układu równa jest R = R1 +R2.
Oporniki R1 i R2 mogą być połączone równolegle i wówczas rezystancja zastępcza układu jest równa 1/R = 1/R1 + 1/R2
Należy napisać predykat obliczający rezystancję układu o dowolnej złożoności np.
resistance(parallel(2, serial( 1, parallel( 1, 2)))).
Obliczanie opiera się na następujących założeniach:
- Jeżeli obliczamy rezystancję ( resistance/2) pojedynczego opornika, to jest ona równa jego oporowi. Ważne, że jest to prawdą tylko w wypadku, gdy opór jest liczbą (a nie np. strukturą).
- Jeżeli w układzie rozpatrujemy połączenie szeregowe (struktura serial/2), to zakładamy, że pierwszy jak i drugi element może być strukturą złożoną (równoległą lub szeregową) i należy obliczyć ich rezystancję zapamiętując ich wynik w pewnych zmiennych. Suma owych zmiennych będzie rezystancją rozpatrywanego układu.
- Jeżeli w układzie rozpatrujemy połączenie równoległe (struktura parallel/2), to zakładamy, że pierwszy jak i drugi element może być strukturą złożoną i należy obliczyć ich rezystancję zapamiętując ich wynik w pewnych zmiennych. Suma odwrotności tych zmiennych będzie odwrotnością rezystancji rozpatrywanego układu.
Problem n-hetmanów
Należy tak rozstawić na pustej szachownicy n (np. 4) hetmanów , by się wzajemnie nie atakowały.
Reprezentacja szachownicy to lista elementów [1/2, 2/3, 3/1, 4/2], co oznacza, że w pierwszej kolumnie hetman znajduje się w drugim wierszu, w drugiej kolumnie w trzecim wierszu itd.
Zapytanie o rozwiązanie ma mieć postać:
solution([1/X1, 2/X2, 3/X3, 4/X4]).
Sieci Bayesa : wnioskowanie
Zadanie opracowane i rozwiązane na podstawie: Ivan Bratko, PROLOG Programming for Artificial Intelligence, Addison-Wesley 2001.
Sieci Bayesowskie w przejrzysty i elegancki sposób pokazują zależności pomiędzy zdarzeniami. Jakie wydarzenia są zależne, a jakie niezależne. Rysunek
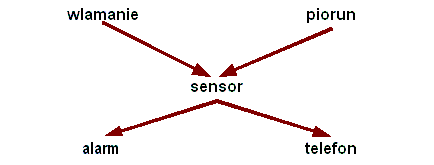przedstawia Sieć Bayesa opisującą złożenie następujących zdarzeń:
- Jeżeli do domu nastąpi włamanie, to wielce prawdopodobne, że uruchomi to sensor.
- Następnie sensor włączy alarm, lub wykona automatyczny telefon ostrzegający.
- Burza z piorunami może prowadzić do takich samych zdarzeń jak włamanie.
Ponadto z sieci można odczytać, że włamanie i piorun są zdarzeniami niezależnymi. Choć, gdy włączy się alarm, to prawdopodobieństwo włamania przestaje być niezależne od pioruna.
Aby reprezentacja była pełna należy podać:
- Prawdopodobieństwo a priori węzłów rodzicielskich (węzłów w korzeniu).
- Prawdopodobieństwa warunkowe dla wszystkich pozostałych węzłów.
Dla podanej na rysunku sieci w pliku ESIsiec_bayesa.pro podane są wszystkie niezbędne do obliczeń prawdopodobieństwa.
Pytanie: Jaką liczbę prawdopodobieństw należy znać dla n zależnych zdarzeń, a jak obliczyć liczbę niezbędnych prawdopodobieństw, gdy wiemy, że pewne zdarzenia są niezależne?
Sieć Bayesa reprezentuje łączny rozkład prawdopodobieństwa. Można zatem obliczyć prawdopodobieństwa dowolnych zdarzeń warunkowych. np.:
p(wlamanie| alarm). p(wlamanie , piorun). p( wlamanie| alarm , nie piorun) p(alarm , nie telefon| wlamanie).
Reguły (wykonywane rekurencyjnie):
- p(X1 ∧ X2 |Warunki) = p( X1 |Warunki) * p(X2 | X1 ∧ Warunki): prawdopodobieństwo iloczynu zdarzeń;
- p(X| Y1 ∧ ... ∧ X ∧ ...) = 1: prawdopodobieństwo zdarzenia pewnego;
- p(X| Y1 ∧ ... ∧nie X ∧ ...) = 0: prawdopodobieństwo zdarzenia niemożliwego;
- p(nie X|Warunki) = 1 - p(X|Warunki): prawdopodobieństwo negacji
- Jeżeli Warunki zawierają potomków zdarzenia X, to stosujemy regułę Bayesa: Jeżeli Warunek0 = Y ∧ Warunki, gdzie Y jest potomkiem X w sieci, to p(X |Warunek0) = p(X|Warunki) * p(Y|X ∧ Warunki) / p(Y|Warunki)
- Jeżeli Warunki nie zawierają potomków X, to
- Jeżeli X nie ma rodziców, to p(X |Warunki)=p(X), gdzie p(X) jest dane;
- Jeżeli X ma rodziców R, to p(X| Warunki) = SUMA(po wszystkich stanach rodzicielskich R) p(X|R1) p(R1|warunki)
Zadanie: Obliczyć ręcznie prawdopodobieństwo włamania, jeżeli wiemy, że włączył się alarm.
Wykorzystać plik ESIbayes.pro do wykonania zadań:
1. Obliczyć prawdopodobieństwo, że włamanie miało miejsce i nie było pioruna, jeśli wiadomo, że alarm zadziałał i nie było telefonu: p(wlamanie i nie piorun | alarm i nie telefon):
prob([wlamanie, nie piorun], [alarm, nie telefon], P).
2. Obliczyć prawdopodobieństwo, że zadziała sensor.
3. Zapytać:
sum_probs([([wlamanie, piorun], 0.9), ([wlamanie, nie piorun], 0.1)], [piorun], P). sum_probs([([wlamanie], 0.9), ([nie wlamanie], 0.1)], [piorun], P).
4. Wyświetlić przodków alarmu.
5. Sprawdzić inne wybrane prawdopodobieństwa.
6. Wymyślić przykład sieci bayesa z większą liczbą węzłów niż 5 dla wymyślonego problemu i przeprowadzić dla niego obliczenia z użyciem programu.
