SE/LS/L2

From WikiZMSI

< SE | LS

Spis treści

[edytuj]

Laboratorium 2 --- Termy, unifikacja, arytmetyka.

[edytuj]

Typy danych i operatory arytmetyczne

Prolog nie wymaga deklarowania typów. Zostaje on rozpoznany ze składni. Plik źródłowy składa się z termów, czyli:

  • atomów: np. ala, x25, x_, x_y, 'Jan Kowalski', 1, -97, 3.14, -0.000035
  • zmiennych: X, Wynik, _x23, specjalna zmienna anonimowa: _.
  • struktur: składają się z kilku komponentów np. data(1, maj, 2004), data(Data, maj, 2004), odcinek(punkt(X,Y), punkt(X1,Y2)), par(r1,seq(r2,r3)).

Lista operatorów arytmetycznych i porównania:

  • + dodawanie
  • - odejmowanie
  • / dzielenie
  • // dzielenie całkowite
  • * mnożenie
  • ** potęga
  • mod reszta z dzielenia
  • is znak równości (wynik obliczeń arytmetycznych) np. ( X is 1 mod 3. )
  • =:= czy wartości równe
  • =\= czy wartości różne
  • > większe
  • < mniejsze
  • >= większe równe
  • =< mniejsze równe
[edytuj]

Zadania (typy danych i operacje arytmetyczne):

1. Na źródle Family.pro wypróbować zapytania: 

parent(X,_).  
mother(_,_). 
mother(X,X).

Jak należy je interpretować?

2. Korzystając ze zmiennej anonimowej dodać do pliku o zależnościach rodzinnych predykaty ma_dziecko/1, który wskaże imię osoby mającej potomstwo i ktos_jest_dziadkiem/0 sprawdzający czy istnieje obiekt spełniający relację dziadek.

3. W nowym pliku zapisać dwa fakty: 

pionowy(odcinek(punkt( X, Y1), punkt( X, Y2))). 
poziomy(odcinek(punkt( X1, Y), punkt( X2, Y))).
  • Jak należy interpretować zapisaną wiedzę?
  • Narysować drzewko dla predykatów umieszczając w korzeniu pionowy lub poziomy. Ile argumentów ma relacja poziomy a ile struktura odcinek itd.
  • Sprawdzić, czy punkty o współrzędnych (1,2) i (1,1) tworzą odcinek pionowy.
  • Jakie współrzędne musi mieć drugi punkt, by tworzył poziomą z punktem (2,3)?
  • Zapytaj o : 
poziomy(odcinek(punkt(2,3),P)).
  • Zapytać czy odcinek rozpoczynający się w punkcie (X1,Y1) i kończący w punkcie (X2,Y2) może być jednocześnie poziomy i pionowy. Czy odpowiedź jest poprawna?

4. Dane są struktury: punkt w 2D p2(X,Y) i punkt w 3D p3(X,Y,Z). Zdefiniować predykat obliczający odległość pomiędzy punktami. np. na zapytanie: 

odleglosc(p2(1,2),p2(3,5),D).

uzyska się odpowiedź: 

D=3,605
[edytuj]

Unifikacja i porównywanie termów

Wpisanie w Prologu (czy to w trybie zapytań, czy w treści reguły) X = ala. oznacza unifikację (uzgodnienie). Co oznacza, że jeżeli można uczynić X i ala równymi to zwracamy sukces, gdy nie, porażkę. Gdy np. operacja == polega na sprawdzeniu równości termów. Sprawdzenie nierówności termów wykonuje się operatorem: \==.

[edytuj]

Zadania z unifikacji i porównywania:

Wypróbować w trybie zapytań działanie: unifikacji i jej negacji(=, \=), równości i nierówności termów (==, \==) oraz przyrównania wartości arytmetycznych (=:=, =\= ): 

X = ala.
X = Y.
ala = ola.
X = data(1, maj, 2004).
data(D, maj, 2003) = data(1, maj, 2004).
data(D, maj, 2003) = data(1, maj, R).
fun(X) = fun(fun(X)).
3 = 3.
1+2 = 3.
1+2 =:= 3.
ala == ala.
X == Y.
X == X.
2+1 == 1+2.
ala \== ola.
odcinek( punkt( 1, 2), punkt( A)) = odcinek( B, punkt( 1, 2)).
odcinek( punkt( 1, 2), punkt( A,B)) = odcinek( B, punkt( 1, C)).
[edytuj]

Program na liczenie największego wspólnego dzielnika

Dane są dwie liczby całkowite dodatnie X i Y. Największy wspólny dzielnik D można określić sprawdzając trzy warunki (trzy reguły):

  1. Jeżeli X i Y są sobie równe, to D jest równe X.
  2. Jeżeli X<Y, to D jest równe największemu dzielnikowi z liczby X i różnicy Y-X. (w Prologu można zapisać jako regułę: nwd(X,Y,D) :- X < Y, Tmp is Y - X, nwd(X, Tmp, D).).
  3. Jeżeli Y<X, to postępujemy jak w punkcie 2 tylko ze zmienioną kolejnością argumentów.

Zdefiniować predykat nwd/3, który będzie spełniony, gdy trzeci argument będzie największym wspólnym dzielnikiem argumentu pierwszego i drugiego. Przykład wywołania: 

nwd(5, 10, X).

Odpowiedzią będzie 

X = 5

Wykorzystaj wbudowany predykat number/1, aby sprawdzać czy term jest liczbą.

[edytuj]

Wyznaczanie ścieżki przejścia w acyklicznym grafie

Dowolny skierowany graf można zdefiniować podając parami łączone węzły. Niech tą relację opisuje predykat krawedz/2 np. 

 krawedz(a,b).

Przykład grafu: 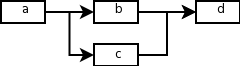Obraz:EsiLabStPrzykladGraf.png Podać strukturę grafu z rysunku lub innego zaproponowanego za pomocą faktów z wykorzystaniem relacji krawedz/2.

Zdefiniować predykat sciezka/2, który będzie sprawdzał, czy istnieje ścieżka pomiędzy podanymi jako argumenty dwoma węzłami w grafie (analogiczne do definicji przodka w zależnościach rodzinnych).

[edytuj]

Zadanie budowanie zdań w j. angielskim

1. W źródle zdanie.pro podany jest mały leksykon i gramatyka z jedną regułą definiującą zadnie.

  • Jakie skonstruować zapytanie, by wygenerować zdania tworzone przez gramatykę z podanego zestawu słów?
  • W jakiej kolejności wygenerowane zostaną te zdania? Zapisz kolejność.


[edytuj]

Małpa i banany

Przy drzwiach stoi małpa, która wchodzi do pokoju. Na środku pokoju wisi pod sufitem banan. Małpa jest głodna i chce dostać banana, ale nie może dosięgnąć go z podłogi. Przy oknie pokoju znajduje się pudło, z którego małpa może korzystać. Małpa może wykonywać następujące czynności:

  • Chodzić po podłodze
  • Wspinać się na pudło
  • Pchać pudlo dookoła (jeśli jest już przy pudełku)
  • Chwycić banana, jeśli stoi na pudełku bezpośrednio pod bananem.

Monkey World jest opisany przez jakiś "stan", który może się zmieniać w czasie. Aktualny stan jest określany przez położenie obiektów:

  • poziome położenie małpy
  • pionowe położenie małpy
  • pozycja pudełka
  • czy ma banana 
  state( MonkeyHorizontal, MonkeyVertical, BoxPosition, HasBanana)

Stan początkowy:

  • Małpa jest przy drzwiach
  • Małpa jest na podłodze
  • Pudełko jest przy oknie
  • Małpa nie ma banana

Kod Prologu reprezentującego stan początkowy: 

state(atdoor, onfloor, atwindow, hasnot).

Stan docelowy to: 

state(_,_,_,has).

Dozwolone ruchy:

  • Chwyć się banana
  • Wejdź na pudło
  • idz od miejsca do miejsca

Nie wszystkie ruchy są możliwe w każdym możliwym stanie świata, np. chwytanie jest możliwe tylko wtedy, gdy małpa stoi na pudełku bezpośrednio pod bananem i nie ma jeszcze banana. 

move( State1, Move, State2)

wykonanie Move zmieni stan State1 na State2.


[edytuj]

Zadanie domowe

1. Do przeczytania: W.F. Clocksin i C.S. Mellish. "Prolog. Programowanie." - Rozdział 2.

2. Zadanie kolorowanie mapy

Stworzyć dowolną mapę terytorialną np.: 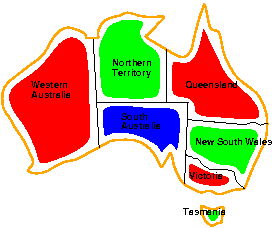Obraz:EsiLabStmapa.png Napisać program, który koloruje mapę z użyciem czterech kolorów, w taki sposób, by dwa sąsiadujące państwa/dzielnice nie miały tego samego koloru (tak jak na rysunku).

Podpowiedź: Państwa(stany) reprezentowane są przez zmienne. Cztery kolory wpisane są jako fakty. Wywołanie poprzez wprowadzenie zapytania np. 

fill(Wester, Northern, South, Queensland, NSW, Victoria, Tasmania).

Kolory powinny być przypisane do państw (odpowiednich zmiennych). Należy wyznaczyć, jakie kraje (stany) nie mogą leżeć obok siebie tj. jakie zmienne nie mogą być sobie równe. Programik jest bardzo ograniczony: działa dla jednej konkretnej mapy

Źródło: "http://wikizmsi.zut.edu.pl/wiki/SE/LS/L2"