SE/LS/L4a

From WikiZMSI

< SE | LS

Spis treści

[edytuj]

Programy w Prologu

Podręcznik do programowania w Prologu i rozwiązywania różnych probelmów ze sztucznej inteligencji zawiera również kody źródłowe.

[edytuj]

Obliczanie oporności układu

Oporniki R1 i R2 mogą być połączone szeregowo i rezystancja zastępcza układu równa jest R = R1 +R2.

Oporniki R1 i R2 mogą być połączone równolegle i wówczas rezystancja zastępcza układu jest równa 1/R = 1/R1 + 1/R2

Należy napisać predykat obliczający rezystancję układu o dowolnej złożoności np. 

res(par(2, ser( 1, par( 1, 2))),W).

Obliczanie opiera się na następujących założeniach:

  1. Jeżeli obliczamy rezystancję ( resistance/2) pojedynczego opornika, to jest ona równa jego oporowi. Ważne, że jest to prawdą tylko w wypadku, gdy opór jest liczbą (a nie np. strukturą).
  2. Jeżeli w układzie rozpatrujemy połączenie szeregowe (struktura serial/2), to zakładamy, że pierwszy jak i drugi element może być strukturą złożoną (równoległą lub szeregową) i należy obliczyć ich rezystancję zapamiętując ich wynik w pewnych zmiennych. Suma owych zmiennych będzie rezystancją rozpatrywanego układu.
  3. Jeżeli w układzie rozpatrujemy połączenie równoległe (struktura parallel/2), to zakładamy, że pierwszy jak i drugi element może być strukturą złożoną i należy obliczyć ich rezystancję zapamiętując ich wynik w pewnych zmiennych. Suma odwrotności tych zmiennych będzie odwrotnością rezystancji rozpatrywanego układu.

Rozwiazanie.pro

[edytuj]

Problem n-hetmanów

Należy tak rozstawić na pustej szachownicy n (np. 4) hetmanów , by się wzajemnie nie atakowały.

Reprezentacja szachownicy to lista elementów [1/2, 2/3, 3/1, 4/2], co oznacza, że w pierwszej kolumnie hetman znajduje się w drugim wierszu, w drugiej kolumnie w trzecim wierszu itd.

Zapytanie o rozwiązanie ma mieć postać: 

template(X), solution(X).

Trzy warianty rozwiązania:

[edytuj]

Sieci Bayesa : wnioskowanie

Zadanie opracowane i rozwiązane na podstawie: Ivan Bratko, PROLOG Programming for Artificial Intelligence, Addison-Wesley 2001.

Sieci Bayesowskie w przejrzysty i elegancki sposób pokazują zależności pomiędzy zdarzeniami. Jakie wydarzenia są zależne, a jakie niezależne. Rysunek 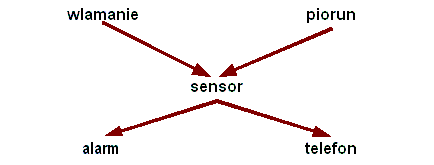Obraz:EsiBayes.gif przedstawia Sieć Bayesa opisującą złożenie następujących zdarzeń:

  • Jeżeli do domu nastąpi włamanie, to wielce prawdopodobne, że uruchomi to sensor.
  • Następnie sensor włączy alarm, lub wykona automatyczny telefon ostrzegający.
  • Burza z piorunami może prowadzić do takich samych zdarzeń jak włamanie.

Ponadto z sieci można odczytać, że włamanie i piorun są zdarzeniami niezależnymi. Choć, gdy włączy się alarm, to prawdopodobieństwo włamania przestaje być niezależne od pioruna.

Aby reprezentacja była pełna należy podać:

  • Prawdopodobieństwo a priori węzłów rodzicielskich (węzłów w korzeniu).
  • Prawdopodobieństwa warunkowe dla wszystkich pozostałych węzłów.

Dla podanej na rysunku sieci w pliku ESIsiec_bayesa.pro podane są wszystkie niezbędne do obliczeń prawdopodobieństwa.

Pytanie: Jaką liczbę prawdopodobieństw należy znać dla n zależnych zdarzeń, a jak obliczyć liczbę niezbędnych prawdopodobieństw, gdy wiemy, że pewne zdarzenia są niezależne?

Sieć Bayesa reprezentuje łączny rozkład prawdopodobieństwa. Można zatem obliczyć prawdopodobieństwa dowolnych zdarzeń warunkowych. np.: 

p(wlamanie| alarm).
p(wlamanie , piorun).
p( wlamanie| alarm , nie piorun)
p(alarm , nie telefon| wlamanie).

Reguły (wykonywane rekurencyjnie):

  1. p(X1 ∧ X2 |Warunki) = p( X1 |Warunki) * p(X2 | X1 ∧ Warunki): prawdopodobieństwo iloczynu zdarzeń;
  2. p(X| Y1 ∧ ... ∧ X ∧ ...) = 1: prawdopodobieństwo zdarzenia pewnego;
  3. p(X| Y1 ∧ ... ∧nie X ∧ ...) = 0: prawdopodobieństwo zdarzenia niemożliwego;
  4. p(nie X|Warunki) = 1 - p(X|Warunki): prawdopodobieństwo negacji
  5. Jeżeli Warunki zawierają potomków zdarzenia X, to stosujemy regułę Bayesa: Jeżeli Warunek0 = Y ∧ Warunki, gdzie Y jest potomkiem X w sieci, to p(X |Warunek0) = p(X|Warunki) * p(Y|X ∧ Warunki) / p(Y|Warunki)
  6. Jeżeli Warunki nie zawierają potomków X, to
    • Jeżeli X nie ma rodziców, to p(X |Warunki)=p(X), gdzie p(X) jest dane;
    • Jeżeli X ma rodziców R, to p(X| Warunki) = SUMA(po wszystkich stanach rodzicielskich R) p(X|R1) p(R1|warunki)

Zadanie: Obliczyć ręcznie prawdopodobieństwo włamania, jeżeli wiemy, że włączył się alarm.

Wykorzystać plik ESIbayes.pro do wykonania zadań:

1. Obliczyć prawdopodobieństwo, że włamanie miało miejsce i nie było pioruna, jeśli wiadomo, że alarm zadziałał i nie było telefonu: p(wlamanie i nie piorun | alarm i nie telefon): 

prob([wlamanie, nie piorun], [alarm, nie telefon], P).
prob(wlamanie, [telefon], P).
prob(wlamanie, [telefon, piorun], P).
prob(wlamanie, [telefon, nie piorun], P).

2. Obliczyć prawdopodobieństwo, że zadziała sensor.

3. Zapytać: 

 sum_probs([([wlamanie, piorun], 0.9), ([wlamanie, nie piorun], 0.1)], [piorun], P).
 sum_probs([([wlamanie], 0.9), ([nie wlamanie], 0.1)], [piorun], P).

4. Wyświetlić przodków alarmu.

5. Sprawdzić inne wybrane prawdopodobieństwa.

6. Wymyślić przykład sieci bayesa z większą liczbą węzłów niż 5 dla wymyślonego problemu i przeprowadzić dla niego obliczenia z użyciem programu.

Źródło: "http://wikizmsi.zut.edu.pl/wiki/SE/LS/L4a"